A permutation is an X-string $S = X_1, X_2, \ldots, X_n$ in which all $X_i$ are distinct.

A combination is a way of selecting several things out of a larger group, where order does not matter.

Permutation with Repetition

The number of n-ary strings of length $k$ are

\[ n \cdot n \cdot … \cdot n ~ \text{(k times}) = n^k \]

Permutation without Repetition

The number n-letter words where no letter used more than once are

\[ P(26, n) = \frac{26!}{(26 - n)!} \]

In general,

$P(m, n)$ := number of permutations of $n$ elements chosen from a set of size $n$

\[ P(m, n) = \frac{m!}{(m - n)!} \]

Circular Permutation

The number of ways to arrange $n$ distinct objects along a fixed circle is

\[ P_n = (n - 1)! \]

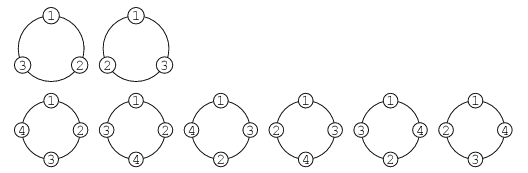
Permutations of sets with some indistinguishable objects

If you have $n$ total objects and $k$ unique objects, call $n_1$ the number of indistinguishable objects of type 1, $n_2$ indistinguishable objects of type 2, … and $n_k$ the number of indistinguishable objects of type $k$, then the number of different permutations of these objects is

\[ {n \choose n_1, n_2, …, n_k} = \frac{n!}{n_1! \cdot n_2! \cdot … \cdot n_k!} \]

Hint: MISSISSIPPI problem. Also known as Multinomial Theorem.

Combination with Repetition

The number of ways to choose a subset of size $k$ from an n-set, allowing repetition, are

\[ {n + k - 1 \choose k - 1} \]

Combination without Repetition

The number of ways to choose a subset of size $k$ from an n-set are

\[ {n \choose k} = \frac{n!}{k! (n - k)!} \]

Proposition:

\[ {n \choose k} = {n \choose n - k} \hskip2em \forall ~ n, k \geqslant 0, k \leqslant n \]

Distributing $n$ distinguishable balls into $k$ distinguishable bins

\[ k^n \]

Distributing $n$ distinguishable balls into $k$ indistinguishable bins

The number of surjections from $n$ to $k$ is

\[ S(n, k) = \sum_{m=0}^k (-1)^m {k \choose m} (k - m)^n \]

Distributing $n$ indistinguishable balls into $k$ distinguishable bins

\[ {n + k - 1 \choose k - 1} \]

Distributing $n$ indistinguishable balls into $k$ indistinguishable bins

The number of integer partitions of an integer $n$ that has $k$ parts. Further reading: Integer Partition.

Binomial Coefficient

Let $x$ and $y$ be real numbers with $x$, $y$ and $x + y$ are non-zero then

\[ (x + y)^n = \sum_{i = 0}^n {n \choose i} x^i y^{n - i} \]